trace-trick
将一个类似 \(x^T A y\) 的标量看作 1x1 trace 然后利用 trace 的性质可以得到 \[ x^T A y = tr(x^T A y) = tr(y x^T A). \]
例题：计算两个多元高斯分布的 KL 散度。
0%
vim备份文件（续）
想不到啊，这学期因为突然断电两次导致写的作业丢了（不过还好丢了 tex 文件但是 pdf 还在不至于重新写）。然后翻备份也没用，不仅工作文件空了，对应的备份文件也空了。vim 自带的 writebackup 也没用。
查了查资料，并且做了几次实验想找到到底在什么条件下文件会丢失，最后的现象是和文件的行为没太大关系，基本上是最后动过的几个文件就会丢失。初步判定是 linux 的“延迟写入”机制导致的。
所以备份不能只备一份，因为备份文件和工作文件是同时保存的，要丢在缓存区基本也是一起丢。只能按照时间对同一个文件建立多个备份。人麻了。
断电真的很危险啊！
FKT算法
大一专业课讲的东西，感觉和 OI 沾点边。
课程资料不方便贴出来，可以参考这个。
前置知识：排列和排列的环分解，矩阵和行列式，图论基本概念。
这篇是介绍一下思想和证明，许多说明性的细节被简要概括了（有空的话再完善细节啥的吧）。
引入
如何求一张图的完美匹配的数量？
以下仅考虑 \(|V|\) （点数）为偶数的图 \(G = (V, E)\) ，记 \(n = |V|\) 和 \(m = |E|\) （边数）。
完美匹配是边集的子集 \(M \subseteq E\)，满足边的端点不重不漏地覆盖了点集。
\(K_n\) 表示 \(n\) 个点的完全图。
记 \(A\) 为 \(G\) 的邻接矩阵，即 \(A_{ij} = 1\) 当且仅当 \((i, j) \in E\) （\(i\) 到 \(j\) 有连边），否则 \(A_{ij} = 0\) 。
一个想法是，枚举 \(K_n\) 的所有完美匹配 \(M\) ，然后判断 \(M\) 的边是否都在原来的图 \(G\) 中，即是否满足 \(M \subseteq E\) 。 记 \(K_n\) 的完美匹配的集合为 \(PM(n)\) ，则 \(G\) 的完美匹配数量为 \[ ans = \sum_{M \in PM(n)} [M \subseteq E] = \sum_{M \in PM(n)} \prod_{(i, j) \in M} A_{ij} \]
举例，如下图。
（当然这玩意直接拿来算是没有意义的）
Pfaffians
判断 \(M \subseteq E\) 的依据是计算 \([M \subseteq E] = \prod\limits_{(i,j) \in M} A_{ij}\) ，这个值只能是 0 或 1 。
如果将 \(M\) 内的边依次写出来，就可以得到一个 \(V\) 的排列 \(\sigma\) ，这个排列的符号（负一的逆序对数次方）记为 \(\mathrm{sgn}(\sigma)\) ，考虑一个类似的式子 \[ \mathrm{wt}(M, \sigma) = \mathrm{sgn}(\sigma) \prod_{i=1}^{n/2} A'_{\sigma(2i-1), \sigma(2i)} \]
其中 \(A'\) 和 \(A\) 略有不同，它是将邻接矩阵的部分 \(1\) 的位置改为 \(-1\) 使得 \(A'\) 成为一个反对称矩阵：\(A'_{ij} = - A'_{ji}\) 。
那么显然 \(|\mathrm{wt}(M, \sigma)| = [M \subseteq E]\) ，因为它们在式子上只有符号的差异。
虽然定义上不仅与 \(M\) 有关，还与选取的排列 \(\sigma\) 有关，但是有趣的是，无论按照什么顺序写边，按照什么顺序写端点得到的 \(\sigma\) ，算出来的 \(\mathrm{wt}(M, \sigma)\) 都是一样的，因此这个值仅仅与 \(M\) 有关，可以记为 \(\mathrm{wt}(M)\) 。
证明：如果交换两条边的顺序，相当于在排列里交换了两个点两次，那么 \(\mathrm{sgn}(\sigma)\) 不变，同时后边的连乘符号也自然不受顺序影响。
如果交换一条边内两个端点的顺序，在排列里交换了两个点，排列的符号变化，同时后边的连乘符号有一项变化，由于 \(A'\) 是反对称矩阵符号又会变一次，因此总的值不变。
假设可以找到一个 \(A'\) 使得 \(\mathrm{wt}(M) = [M \subseteq E]\) ，那么要求的值变成了 \[ ans = \sum_{M \in PM(n)} \mathrm{wt}(M) \]
上式称为 \(A'\) 的 Pfaffian ，记为 \(\mathrm{Pf}(A')\) 。
反对称矩阵行列式
考虑反对称矩阵 \(A'\) 的行列式 \[ \det(A') = \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma) \prod_{i=1}^n A'_{i,\sigma(i)} \]
如果 \(\sigma\) 存在 \(i\) 使得 \(\sigma(i) = i\) （环分解有自环），那么 \(A_{i,\sigma(i)} = 0\) ，这一项是没有贡献的。
如果 \(\sigma\) 的环分解存在一个非自环的奇环，那么将这个奇环的方向反过来得到 \(\sigma'\) ，注意到 \(\mathrm{sgn}(\sigma) = \mathrm{sgn}(\sigma')\) 且连乘符号的值相反，将 \(\sigma\) 和 \(\sigma'\) 两两一组，每组在行列式中的贡献为 \(0\) 。
综上，我们只需要考虑偶环构成的排列的贡献，记 \(EC(n)\) 是这些排列，有 \[ \det(A') = \sum_{\sigma \in EC(n)} \mathrm{sgn}(\sigma) \prod_{i=1}^n A'_{i,\sigma(i)} \]
而仅有偶环构成的排列和 \(K_n\) 中完美匹配的二元组 \((M_1, M_2)\) 是一一对应的！
将 \(M_1\) 和 \(M_2\) 直接并起来就可以得到一个偶环组成的排列 \(\sigma\) ，其中每个偶环都是由 \(M_1\) 和 \(M_2\) 的边交替构成。偶环上边的方向怎么确定？每个环选定环上编号最小的点，指向 \(M_1\) 中的连边。
注意：\(M_1\) 和 \(M_2\) 的公共边在 \(\sigma\) 中体现为两个点之间的重边组成的二元环。
类似地每个偶环组成的排列 \(\sigma\) 也可以拆分成两个完美匹配 \(M_1, M_2\) 。
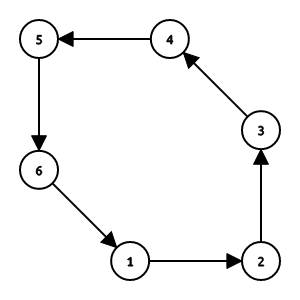
如上图，找到偶环编号最小的点 \(1\) ，然后其指向 \(2\) ，那么 \((1, 2) \in M\) 。然后沿着这个方向把边交替加入 \(M_1, M_2\) 。最终可以知道，这个排列对应的两个匹配为 \[ M_1 = \{(1, 2), (3, 4), (5, 6)\}, M_2 = \{(2, 3), (4, 5), (6, 1)\} \]
这个一一对应关系告诉我们 \(|EC(n)| = |PM(n)|^2\) ，并且枚举 \(\sigma \in EC(n)\) 等价于枚举 \(M_1, M_2 \in PM(n)\) ，于是 \[ \begin{aligned} \det(A') &= \sum_{M_1 \in PM(n)} \sum_{M_2 \in PM(n)} \mathrm{sgn}(\sigma) \prod_{i=1}^n A'_{i,\sigma(i)} \\ &= \sum_{M_1 \in PM(n)} \sum_{M_2 \in PM(n)} \mathrm{sgn}(M_1) \mathrm{sgn}(M_2) \prod_{i=1}^n A'_{i,\sigma(i)} \\ &= \sum_{M_1 \in PM(n)} \sum_{M_2 \in PM(n)} \mathrm{wt}(M_1) \mathrm{wt}(M_2) \\ &= \mathrm{Pf}(A')^2 \end{aligned} \]
（这个等式可以拿上面的例子写一写就很容易明白）
Pfaffian orientation: 找到反对称矩阵
现在我们知道 \(ans = \mathrm{Pf}(A') = \sqrt{\det(A')}\) ，而求行列式是容易的。
但不要忘了第一个等号建立在一个假设上：\(\mathrm{wt}(M) = [M \subseteq E]\) 。现在我们要关注如何找到满足这个条件的 \(A'\) 。
找一个 \(A'\) 等于是给 \(G\) 的边定向，然后把邻接矩阵中正向的定为 \(1\) ，反向的定为 \(-1\) 。我们的目标是让所有 \(G\) 中的完美匹配 \(M\) 满足 \(\mathrm{wt}(W) = 1\) （或全部是负一，这个时候 \(ans = -\mathrm{Pf}(A') = \sqrt{\det(A')}\) ，不影响）。
那么就是让所有 \(G\) 的完美匹配 \(M_1, M_2\) 满足 \(\mathrm{wt}(M_1) \mathrm{wt}(M_2) = 1\) 。上一节的推导告诉我们 \[ \mathrm{wt}(M_1) \mathrm{wt}(M_2) = \mathrm{sgn}(\sigma) \prod_{i=1}^n A'_{i, \sigma(i)} \] 其中 \(\sigma\) 是 \(M_1, M_2\) 对应到的那个偶环构成的排列。
于是我们的要求变为：对于 \(G\) 内任意偶环 \(C\) ，设这个偶环单独构成的排列为 \(\sigma\) ， 如果 \(G - C\) 存在完美匹配，那么就要有 \[ \prod_{i=1}^n A'_{i, \sigma(i)} = -1 \]
（注意到每个偶环的符号恰为 \(\mathrm{sgn}(\sigma) = -1\) ）。
这个要求是我们目的（\(\mathrm{wt}(M_1) \mathrm{wt}(M_2) = 1\)）的充要条件。如果满足了这个要求，那么对于任意偶环构成的排列，将其分解成若干偶环的乘积，从这个要求中可以知道每个偶环的贡献，进而知道偶环构成的排列的贡献恰为 \(1\) 。
如果满足了我们的目的，那么对于任意偶环 \(C\) ，如果 \(G - C\) 存在完美匹配，说明有一个偶环构成的排列包含了 \(C\) ，让 \(C\) 以外的部分全是二元环就可以从 \(\mathrm{wt}(M_1) \mathrm{wt}(M_2) = 1\) 中推出上式（因为每个二元环的贡献都显然是 \(1\) ）。
而上式等价于 \(C\) 里面有奇数个顺时针的边和奇数个逆时针的边。
对于一般图这是 #P-Hard 的问题，我们考虑特殊的情况：平面图。
平面图上只需要满足每个面都有奇数条顺时针的边即可。
可以归纳出任何简单环 \(C\) 都满足：顺时针的边数 \(f\) 加上环内部的点（平面上被环围起来的点）数 \(k\) 恰为奇数。
如果 \(C\) 是一个面那么 \(k = 0\) ，这就是我们需要满足的要求。
否则在 \(C\) 内找一条路径把 \(C\) 切成两个环 \(C_1, C_2\) 。\(C\) 是 \(C_1, C_2\) 的对称差，根据归纳假设可以知道 \(f + k\) 为奇数。
现在考虑偶环 \(C\) 。如果 \(G - C\) 有完美匹配那么 \(C\) 的内部必须有偶数个点，于是顺时针的边数必须奇数，证毕。
现在这个问题是相对容易的，任意找一个生成树任意定向，然后就可以逐个确定非树边的方向。
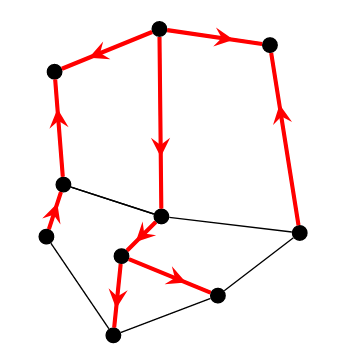
上图找到了一颗生成树 \(T_1\) 并给了一个任意的定向。
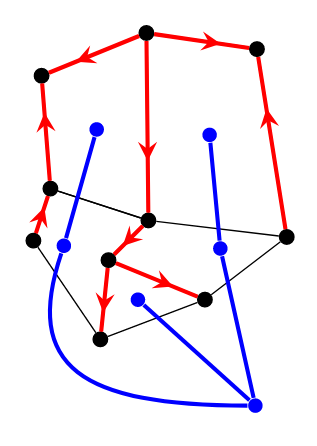
上图找了对偶图的一棵与 \(T_1\) 不相交的生成树 \(T_2\) （这一步在手算定向时可以省略，因为可以肉眼看出哪些非树边可以被定向）。
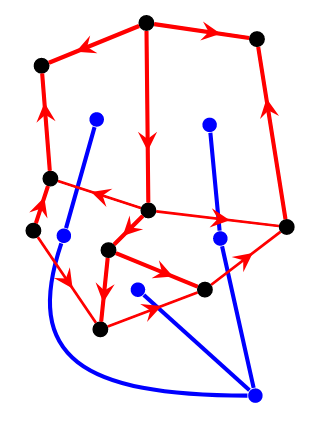
上图从 \(T_2\) 的叶子开始逐步确定 \(G - T_1\) 的定向，使得每个面上都恰有奇数条顺时针边。
踩坑杂记
总是踩坑，有的时候一个坑或者原理类似的坑还反复踩，踩麻了所以记录一下。
也不一定是踩坑，也包括一些折腾日记，自用。
Hexo 报错：expected end of comment, got end of file (2022.02.27)
{# 是 nunjucks 的注释，写 tex
的时候出现了个这个就挂了
Manjaro 终端输入卡顿延迟 (2022.03.15)
compton 的锅，要加 --xrender-sync-fence
参数，之前好过一段时间没管结果更新系统后又出现了。
yay 使用 tuna 源而无法更新 aur (2022.05.24)
Tuna 很早就移除了 aur 镜像， 将 aur 源修改为官方源的方法为：
1 | yay --aururl "https://aur.archlinux.org" --save |
但是切换后更新部分软件包仍会出现报错，如更新 wps-office 时：
1 | (数据已丢失) |
不难发现仍然用到了 tuna 源。我一开始不能理解，后来在Github 上找到了一点线索，原来是 cache 导致的问题。
在 yay 的 cache 目录下进入 wps-office 的仓库，查看
git --remote 可以看到远程仓库指向的是 tuna 的地址。
解决方法：修改远程仓库地址，或者直接清理掉 cache 。前者有人给出了批处理脚本
pacman 更新报错「GPGME 错误：无数据」 (2022.05.29)
原因是下载 .sig 文件的时候被登陆网页劫持了，解决方案为
sudo rm /var/lib/pacman/sync/*.sig 。
编译 grpc 报错：fatal error: Killed signal terminated program cc1plus (2022.06.01)
原因是 make -j 并行编译占用内存过多（直接飙升到十几 G
吃满内存然后挂了）。
之前不知道这个参数的含义就用了，所以看到内存崩了心态也崩了。
解决方法：限制并行数量，如 make -j4
（根据实际情况调整，不然确实挺慢的）。
vim备份文件
由于我在 linux 的主目录自动挂载一个 tmp ，然后习惯有啥乱七八糟的文件都在这个 tmp 里面操作。 坏处之一是这里头的文件断电不保存（tmp 挂在内存上），而且有些需要保存的文件我也习惯往里头写。 于是在一次记笔记的时候，在 tmp 里写完忘记拷贝出去了，之后写作业才发现我笔记不见了。
第一个想到的是通过 vim 的 undo histroy 来复原文件，虽然的确可以看到一些文件内容， 但是是无法还原整个文件的。
查的时候发现我以前也查过这个问题，然后想起来我之前就遭遇过这样的损失， 为了避免重蹈覆辙给 vim 加了个备份功能。 于是翻了我备份的源码，去备份目录找，果然还在，虚惊一场。
附备份代码 (vim script) ：
1 | function s:Make_Dir () |
参考页面：
计算机应用数学学习笔记
\(\newcommand{\bR}{\mathbb{R}}\) \(\newcommand{\OV}{\overline}\)
上半期太摸了，没记。
抽象代数学习笔记
\(\newcommand{\bbZ}{\mathbb{Z}}\) \(\newcommand{\bbQ}{\mathbb{Q}}\) \(\newcommand{\bbN}{\mathbb{N}}\) \(\newcommand{\bbF}{\mathbb{F}}\) \(\newcommand{\bbR}{\mathbb{R}}\) \(\newcommand{\bbC}{\mathbb{C}}\) \(\newcommand{\Colon}{\colon\;}\) \(\newcommand{\Inner}[1]{\langle #1 \rangle}\) \(\newcommand{\List}[2]{ { #2}_{1}, { #2}_{2}, \ldots, { #2}_{ #1} }\) \(\newcommand{\Aut}{\mathrm{Aut}}\) \(\newcommand{\Inn}{\mathrm{Inn}}\) \(\newcommand{\Char}{\;\mathrm{char}\;}\) \(\newcommand{\divide}{\mid}\) \(\newcommand{\ndivide}{\nmid}\) \(\newcommand{\Hom}{\mathrm{Hom}}\) \(\newcommand{\ch}{\mathrm{ch}}\) \(\newcommand{\Up}{\overline}\) \(\newcommand{\Gal}{\mathrm{Gal}}\)
Preliminaries
equivalence relation
Definition. A binary relation on a set \(A\) is a set \(R \subseteq A \times A\). We denote \((a, b) \in R\) by \(a \sim b\).
Definition. A binary relation \(R\) is an Equivalence relation iff it is
- reflexive: \(a \sim a\).
- symmetric: \(a \sim b \implies b \sim a\).
- transitive: \(a \sim b \land b \sim c \implies a \sim c\).
Definition. For a equivalence relation on \(A\), the equivalence class of \(a \in A\) is defined to be \([a] = \{x \in A \Colon x \sim a\}\) (or denoted by \(\bar{a}\)).
Definition. If \(C\) is an equivalence class, any element \(c \in C\) is called a representative of \(C\).
Definition. A partition of a set \(A\) is a collection \(P = \{A_i | i \in I\}\) of nonempty subsets of \(A\) s.t.
- \(A = \cup_{i \in I} A_i\)
- \(A_i \cap A_j = \emptyset\) for all \(i, j \in I\) with \(i \ne j\).
If \(P\) is a partition of \(A\) we also say that \(P\) partitions \(A\).
The collection of all equivalence classes is a partition.
微积分/数学分析笔记四（积分）
\(\newcommand{\bbR}{\mathbb{R}}\) \(\newcommand{\bbN}{\mathbb{N}^+}\) \(\newcommand{\Lim}{\lim\limits_}\) \(\newcommand{\Sum}{\sum\limits_}\) \(\newcommand{\eps}{\varepsilon}\) \(\newcommand{\Colon}{\colon\;\;}\)
数分肯定是学不动了，所以按微积分的学习进程来，但是概念可能只要参考数分。
一些理论
黎曼积分
对于闭区间 \([a, b]\) ，选取有限的若干点
\[ a = x_0 < x_1 < x_2 < \ldots < x_n = b \]
称为该区间的一个分割 \(P\) 。\(\lambda(P) = \max\{x_i - x_{i-1}\}\) 称为分割参数。
选取 \(n\) 个标记点 \(\xi_i \in [x_{i-1}, x_i]\) ，称 \((P, \xi)\) 构成一个标记分割。
令集合 \(\mathcal P\) 表示所有标记分割的集合。令集合族 \(\mathcal B\) 包含所有集合 \(B_d = \{(P, \xi) | \lambda(P) < d\}\) 其中 \(d > 0\) 。那么 \(\mathcal B\) 是一个滤子基。
为了方便直接用 \(\lambda(P) \to 0\) 表示这个滤子基。
对于在 \([a, b]\) 有定义的函数 \(f\) 。定义积分和为
\[ \phi(P, \xi) := \sum_{i=1}^n f(\xi_i) (x_i - x_{i-1}) \]
那么黎曼积分可以定义为：
\[ \int_a^b f(x) dx := \Lim{\lambda(P) \to 0} \phi(P, \xi) \]
线性代数笔记（一）
\(\newcommand{\Span}{\operatorname{span}}\) \(\newcommand{\Nullity}{\operatorname{nullity}}\) \(\newcommand{\Rank}{\operatorname{rank}}\) \(\newcommand{\Colon}{\colon\;\;}\) \(\newcommand{\Inner}[1]{\langle #1 \rangle}\) \(\newcommand{\Norm}[1]{\lVert #1 \rVert}\) \(\newcommand{\List}[2][n]{\{ #2_1, #2_2, \ldots, #2_#1 \}}\)
Chap. 1
vector spaces
域 (field) \(F\) 上的向量空间 (vector space over \(F\)) 或线性空间 (linear space) \(V\) 包含一个向量集合和两个运算 (addition and scalar multiplication) 满足：
- 加法交换律 (commutativity of addition) 。
- 加法结合律 (associativity of addition) 。
- 有加法单位元。
- 每个向量有加法逆元。
- 有乘法单位元。
- 乘法结合律。
- 乘法对加法有分配律，\(a (x + y) = ax + ay\) 以及 \((a + b) x = ax + bx\) 。
其中加法是向量加法，乘法是 \(F\) 上的标量乘向量（标乘）。
计算机入门学习笔记（一）
我全程摸鱼，妈的计入门杀我。