牛客练习赛57

咕咕咕我又来写总结啦。

第一次打牛客，一进牛客发现还有 30s 就有一场比赛，就报了名。
一开始只是打算玩玩，看看牛客的题来着。

牛客

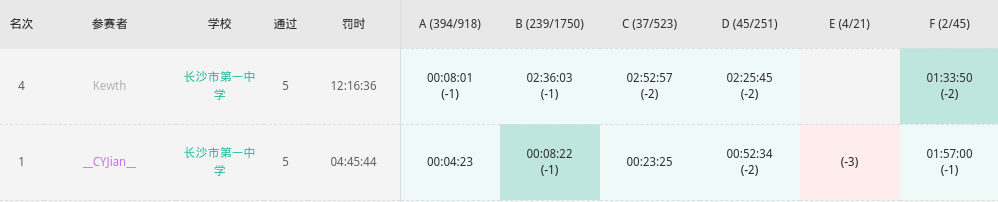
一不小心上瘾了，可惜不计 rating 。
（另外 %%% @CYJian 喜提 rank1 ）

先看 A 题挺签到的，花几分钟过了，然而交 WA 了一次，原因竟然是下标 0, 1 开头混用了，感觉自己很蠢。

然后想着玩玩嘛，就直接开 F 了。

嗯看着是道数学题？这个求和方式是个组合数嘛，询问就是一个这玩意：

\[\sum_{i=l}^r a_i C_{r-l}^{i-l}\]

我猜这个个组合数展开成阶乘然后配卷积，然后推式子，推了一年没有半点用，连个卷积的影子都没有。

然后打算根据组合意义算，就是在一个三角形上走的路径数，
三角形有 \(O(n^2)\) 个点，每个点可以 \(O(1)\) 递推 (\(A_{i,j} = A_{i-1,j} + A_{i-1,j-1}\)) ，
询问就是询问一个点的值 (\(A_{r,r-l}\)) 。
但同时根据组合数的性质，每个点可以 \(O(k)\) 地由该点底下 k 层的 k 个点递推出来。
暴力预处理是 \(O(n^2+q)\) 的，暴力询问是 \(O(n+qn)\) 的，这看着就是要在两者之间求得平衡。

于是我想到了分块，只要预处理三角形若干排，然后询问就可以找到比较近的已经处理的一排暴力算。

如果两排的间距是 \(B\) ，那么询问复杂度就是 \(O(B)\) 的。

然而怎么预处理？每个点拿组合数直接算复杂度仍然是 \(O(n^2)\) 的 🤔 。

然后卡这里又卡了一年，后来灵光一现发现两排之间的生成函数就是乘一个 \((1+x)\) ，
用 NTT 即可在两排之间快速预处理，乘一个 \((1+x)^B\) 就行了。
\((1+x)^B\) 不就是是组合数的生成函数吗？这都没想到感觉自己很睿智。

那么预处理的复杂度为 \(O(nlogn\frac{n}{B})\) 的，和询问的复杂度均衡一下就可以得到一个 \(O(n\sqrt{nlogn})\) 的做法。
（假定 \(n, q\) 同阶）

然后就开始码，码完 T 了，T 了两次，经 @CYJian 指点发现 \(B\) 设小了，导致带 log 的卷积部分跑得很慢。
改完就 A 了，过了 1.5h 竟然还拿了一血。
这个时候没记错是 rank140 左右。

然后开了一眼 D 感觉就是个马拉车，打完发现疯狂 WA ，仔细读题发现要求找两个子串，是恰好两个，用一个都不行 wdnmd 😡 。

A 掉 D 就开始飘了， B 题细节题屑的一批，C 题是个 FWT 。

结果 C 题也疯狂 WA ：

	while(T --) {
		// ....
		for(int i = 0; i < n; i ++)
			if(w[i] > W) {
				puts("No");
				continue;
			}
		// ....
	}
}

原因竟然是这个特判，它的 continue 只对 for 有效。。。
都打了两三年代码竟然犯这个错误。。。

最后打完就只有几分钟了，竟然上了 rank4 ，罚时高出天际。

没有被抽中 😭 😭 😭 😔 😔 😔 。