一类不公平博弈总结
以下简称超现实数 Surreal Numbers 为 SN 。
超现实数完整的理论很复杂,这里不详细给出。
超现实数与游戏
一个 SN 可以表示为 \(P = \{S_L|S_R\}\) ,其中 \(S_L\) 和 \(S_R\) 都是 SN 的集合。
若 \(P\) 是 SN ,需要满足一个公理:
\[\forall X \in S_L, Y \in S_R, X \ngeq Y\]
这样定义 SN 的偏序关系,\(P = \{S_L|S_R\} \le Q = \{T_L|T_R\}\) 当且仅当以下两点同时成立:
\[\forall X \in S_L, X \ngeq Q\] \[\forall Y \in T_R, Y \nleq P\]
一个游戏 \(P\) 可以类似地对应到一个 SN ,其中 \(S_L\) 是左玩家能够转移到的游戏的集合,\(S_R\) 是右玩家能够转移到的集合。
简单的情况
不加证明的给出以下重要的性质,实践中往往将 SN 用普通的实数表示,当然不是所有 SN 都能对应到一个实数的,实数域只是超现实数域的一个子集。
- 对于 SN \(P = \{|\}\) ,有 \(P = 0\) ,即加法单位元。
- 对于 SN \(P = \{S_L | S_R\}\) ,如果集合 \(S_L\) 存在最大值 \(P_L\) ,则 \(P = \{P_L | S_R\}\) 。
- 对于 SN \(P = \{S_L | S_R\}\) ,如果集合 \(S_R\) 存在最小值 \(P_R\) ,则 \(P = \{S_L | P_R\}\) 。
- 对于 SN \(P = \{P_L | P_R\}\) ,\(P\) 的值可以由一颗特殊的树确定,\(P\) 是值在 \(P_L\) 和 \(P_R\) 之间的最浅的点(不包括 \(P_L, P_R\) ),这棵树长这样:
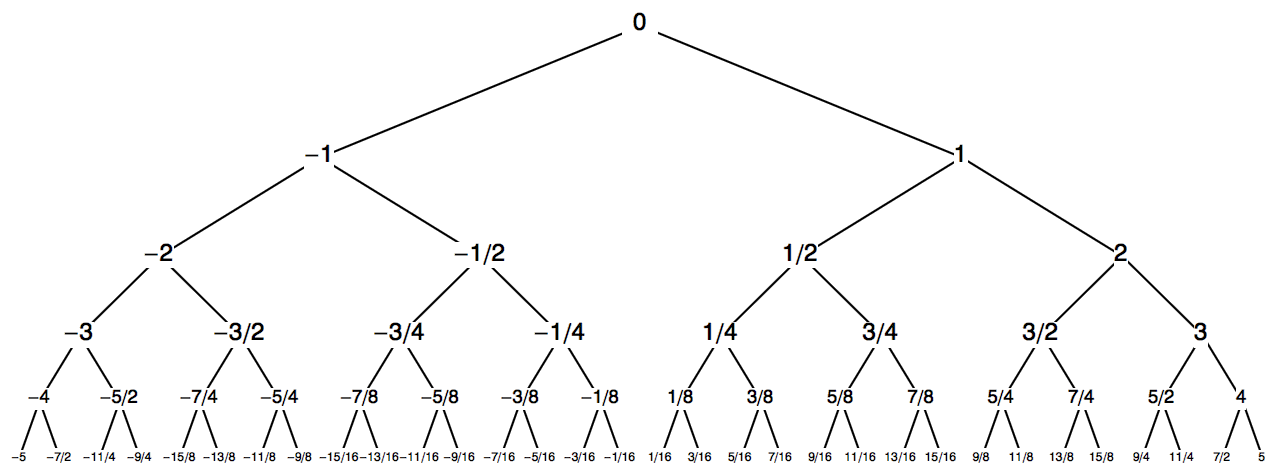
- 对于 SN \(P = \{P_L |\}\) ,\(P\) 是值大于 \(P_L\) 的最浅的点。
- 对于 SN \(P = \{| P_R\}\) ,\(P\) 是值小于 \(P_R\) 的最浅的点。
直观上,可以将一个能对应到实数的 SN 理解为左玩家可以自由操作的次数减去右玩家可以自由操作的次数。
一个游戏可以看做一个 SN \(P\) :
- 如果 \(P > 0\) ,那么左玩家必胜。
- 如果 \(P < 0\) ,那么右玩家必胜。
- 如果 \(P = 0\) ,那么先手必败。
- 如果 \(P\) 和 \(0\) 没有偏序关系,那么先手必胜(这个情况稍后讨论)。
以上四点的逆命题也是成立的。
如果一个游戏 \(P\) 可以划分为若干互不影响的子游戏 \(P_1, P_2 ... P_n\) ,那么 \(P = P_1 + P_2 + ... + P_n\) 。
和 0 可以确定偏序关系的 \(P\) 可以简单的加起来,但是和 0 没法确定偏序关系的一些 \(P\) 的加法比较特殊。
例如公平博弈下的 SG 定理,子游戏的加是 SG 值的异或,事实上公平博弈的游戏对应的 SN 只能是 0 或者是与 0 没有偏序关系的数。
其他的一些性质:
- 对于 SN \(P = \{P_L|P_R\}\) ,其加法逆(相反数)为 \(-P = \{-P_R|-P_L\}\) 。
更复杂的情况
之前提到过,有些游戏状态对应的 \(P\) 和 \(0\) 没有偏序关系。
这里要引入三个基本的量:\(\star = \{0|0\}, \uparrow = \{0|\star\}, \downarrow = \{\star|0\}\) 。
不难看出 \(\star\) 实际上就不满足 SN 的公理,但是这三个量确实对应于一些游戏的状态,因此为了更好的研究这类特殊的博弈,这些量的引入是必须的。
不加证明的给出以下性质:
\(\star\) 小于所有正实数且大于所有负实数,与 0 没有偏序关系。
\(\uparrow\) 小于所有正实数且大于 0 。
\(\downarrow\) 大于所有负实数且小于 0 。
\(\star + \star = 0\) ,也就是说 \(\star\) 的逆是其本身。
\(\{\uparrow|\downarrow\} = \{\uparrow|0\} = \{0|\downarrow\} = \star\)
\(\{\downarrow|\uparrow\} = 0\)
\(\forall X \in R, \{X|X\} = X + \star\) ,通常记做 \(X\star\) ,\(X = 0\) 时与 0 没有偏序关系,否则 \(X\star > 0\) 当且仅当 \(X > 0\) 。
另外,对于 SG 值为 \(X\) 的公平博弈,其值可以记做 \(\star X\) ,它的加法就是 \(X\) 的异或,\(X\) 不为 0 时该数与 0 没有偏序关系。
可以从这些量的角度研究博弈,同样可以从博弈的角度研究这些量。
例如要证明 \(\{\uparrow|\downarrow\} = \star\) ,可以证明其等价命题 \(\{\uparrow|\downarrow\} + \star = 0\) ,即证明该游戏先手必败,这通过简单的博弈归纳是很容易证明的。
其他的一些性质:
- \(\{0|\uparrow\} = \uparrow + \uparrow + \star\)
- \(\{\downarrow|0\} = \downarrow + \downarrow + \star\)
更更复杂的情况
然而即使有了 \(\star\) ,许多游戏仍然无法被表示,例如 \(\{1|-1\}\) ,它也有一些性质,例如它的加法逆是它本身。
由于游戏 \(P\) 对应的 \(\{S_L|S_R\}\) 与超现实数不同,不受公理的限制,这似乎预示了不是无法所有问题都能拿超现实数获得满意的结果的,超现实数能解决的终究是一部分较为特殊的问题。
例如 Nim 游戏的 mex 规则和 SG 定理,这些东西直接拿超现实数或是 \(\star\) 这些东西是无法解释的。
因此,还是要具体问题具体分析。
推荐读物
这里只是总结,希望具体了解超现实数和博弈的关系的话可以去看这些东西。