好题题解整理(一)
没有摘要。
th1690-a
给定一个 \(n\) 个点的竞赛图,求一个 \(m\) 边染色方案。(\(n=3000, m=14\) )
竞赛图是任意一对点都有恰好一条有向边的有向图。
题解
这样转换问题:允许边染上多种颜色,给每个点 \(u\) 一个颜色集合 \(S_u\) ,对于一条边 \((u, v)\) ,它染上颜色 \(c\) 当且仅当 \(c \in S_u \wedge c \notin S_v\) 。
这样一来很容易给出一个构造方案:把大小恰为 \(\frac{m}{2}\) 的颜色集合任意分配给每个点即可。这样任意一对点 \(u, v\) 都存在一个 \(u\) 拥有而 \(v\) 没有的颜色。并且有 \(\dbinom{m}{\frac{m}{2}} \ge n\) 。
th1690-b
有一张 \(n\) 个点的无向图满足任意一个导出子图都存在一个度数不超过 \(k\) 的点。每次可以询问一个点集是否有边,如果有会给出任意一条,要求用 \(n(2k+1)\) 次询问求出边集。其中 \(n\) 是已知量,\(k\) 是未知量。
题解
这个 \(k\) 的限制很奇怪,很难得到直接有效的性质,需要敏锐的观察力。
引理 1
每次在图中找到度数最小的点删除,删除的点按顺序构成一个序列,在该序列中从前向后连边得到新图,新图中每个点的出度不超过 \(k\) 。
应用反证法,如果新图存在一个度数大于 \(k\) 的点,设该点的闭合子图的点集为 \(S\) ,可以发现 \(S\) 在原图中是一个每个度数都超过 \(k\) 的导出子图,矛盾。
引理 2
这张图可以 \(k+1\) 染色。
根据引理 1 提到的序列,把该序列从后往前染色,由于每个点出度不超过 \(k\) ,染色数不会超过 \(k+1\) 。
引理 3
图的边数不超过 \(nk\) 。
根据引理 1 提到的序列可以简单得出,注意引理 1 提到的新图和原图边数相等。
正题
有了三个强大的引理就可以做题了。
维护染色集合,逐个加入每个点 \(u\) 并求出 \(u\) 与已加入的点之间的边。加入点 \(u\) 时和每个染色集合放一起询问。如果询问得到了一条边,该边一定包含 \(u\) ,因为一个染色集合是一个独立集,这时候把该边另外一个点在询问集合里去掉继续询问,直到询问出来没有边。
然后就得到了当前已经加入的点的导出子图,每次求出引理 1 提到的序列并用引理 2 的方法重新染色,复杂度 \(O(n^2k)\) 。
询问的次数不超过 \(n|C| + |E|\) ,其中 \(|C|, |E|\) 分别是染色数和边数。根据引理 2 和引理 3 ,询问次数不超过 \(n(2k+1)\) 。
th1689-b
给定 \(k\) 次多项式的 \(k+1\) 个点值 \(f(0)\) 到 \(f(k)\) ,对于正整数 \(q, n\) 求 \(\sum_{i=1}^n f(i)q^i\) \((q\neq{1})\) 。
时间复杂度:\(O(k+\log{n})\) 。
题解
设 \(S(m) = \sum_{i=0}^{m-1} f(i) q^i\) 。
引理 1
存在 \(k\) 次多项式 \(G\) 满足 \(S(m) = q^m G(m) - G(0)\) 。
对 \(k\) 应用数学归纳法。对于 \(k=0\) 不难证明。对于 \(k \ge 1\) ,对 \(S(m)\) 和 \(q S(m)\) 作差,设 \(g(i) = f(i) - f(i-1)\) ,显然 \(g\) 是 \(k-1\) 次多项式。那么根据归纳假设,存在 \(k-1\) 次多项式 \(P\) 满足 \(\sum_{i=0}^{m-1} g(i) q^i = q^m P(m) - P(0)\) ,于是可以得到:
\[(1-q)S(m) = q^m P(m) - P(0) + f(-1) - q^m f(m - 1)\]
从中不难得到这样一个 \(k\) 次多项式 \(G(m) = \dfrac{P(m) - f(m - 1)}{1 - q}\) 。
正题
根据引理 1 ,我们可以通过求 \(G(n+1)\) 和 \(G(0)\) 间接求出 \(S(n+1)\) 。
然而对于 \(G\) 我们知道的只有它的次数和它与 \(S, f\) 的关系,所以求 \(G\) 仍然要从 \(S, f\) 下手。
比如对 \(S\) 作差可以间接对 \(G\) 作差,得到 \(qG(m+1) - G(m) = f(m)\) ,这是个递推关系。
那么通过已知的 \(f\) 的点值和这个递推关系可以得到 \(k+1\) 个方程和 \(k+2\) 个变量,还差一个就可以解方程。
我们还没有用到 \(G\) 的多项式次数为 \(k\) 这个性质,把 \(G\) 做 \(k+1\) 次差分便可再得到一个方程:
\[\sum_{i=0}^{k+1} G(i) \binom{k+1}{i} (-1)^i = 0\]
线性消元即可解出 \(G(0)\) 到 \(G(k+1)\) ,然后线性拉格朗日插值即可得到 \(G(n+1)\) 。
lg4548
按如下方式随机生成一个序列:每次等概率在序列末尾添加一个 \(1\) 到 \(n\) 的正整数,当长为 \(m\) 的给定序列 \(\{a\}\) 成为随机序列的子串时停止。求该随机序列的期望长度。
时间复杂度:\(O(m)\) 。
题解
似乎是道论文题,比较偏数学,代码没几行。
设 \(X\) 表示随机序列的期望长度,其 PGF 为 \(F(x)\) 。
常识:\(E(X) = F'(1)\) 。
设 \(g_k\) 表示序列长度为 \(k\) 时仍然没有停止的概率,即 \(P(X>k)\) ,其 OGF 为 \(G(x)\) 。
常识:\(F'(1) = G(1)\) 。
如果序列长 \(k\) 时仍未停止,考虑如果直接在后面添加序列 \(\{a\}\) ,一定会结束,但最后的长度未必恰好是 \(k+m\) ,可能是任意的 \(k+i\) ,其中 \(i\) 是序列 \(\{a\}\) 的一个 border 长度。
于是可以得到 \(G(x) (\frac{x}{n})^m = \sum_{i\in{S}} F(x) (\frac{x}{n})^{m-i}\) ,其中 \(S\) 是 border 长度集合。
代入 \(x=1\) ,有 \(G(1) = \sum_{i\in{S}}F(1) n^i\) ,\(F(1)=1\) 也是常识,于是 KMP 求出 \(S\) 后就可以算出 \(G(1)\) 。
cf643f
有 \(n\) 个人和若干个桶,每一天每个人会选一个桶的集合并品尝。有恰好一个桶有毒,品到毒的人立即晕倒,人们以身试毒,确定哪个桶有毒,同时希望晕倒人数不超过 \(p\) 。
设 \(R_i\) 表示试毒进行 \(i\) 天,最坏情况下人们最多能在多少桶中找到毒,求出 \(R_1\) 到 \(R_m\) 。
时间复杂度:\(O(pm)\) 。
题解
(未实现)
给每个人选一个桶的集合不好处理,不妨给每个桶选一个被品尝的集合 \(S\) ,首先必须满足 \(|S| \le p\) ,否则该桶有毒会直接导致失败。
那么 \(R_1\) 的值就呼之欲出了,由于只进行一天,必须给每个桶分配一个不同的集合,否则无法区分集合相同的桶,那么答案就是集合的数量: \(\sum_{i=0}^p \binom{n}{i}\) 。
推广到更一般的情况,试毒假设进行 \(t\) 天,对于一个集合为 \(S\) 的桶,如果该桶是毒,那么第一天过后人们就只需要在集合恰为 \(S\) 的所有桶中尝试,并且会增加 \(|S|\) 名晕倒人数。
于是可以设计 DP ,设 \(f_{i,t}\) 表示已经晕倒 \(i\) 人,试毒还剩 \(t\) 天的情况下人么最多能从多少桶中找到毒,可以得到转移:
\[f_{i,t} = \sum_{j=0}^{p-i} \binom{n-i}{j} f_{i+j,t-1}\]
初值是 \(f_{i,0}=1\) 。这个 DP 的复杂度是 \(O(p^2m)\) 的,不难发现是卷积形式,可以优化到 \(O(mp\log{p})\) ,但还是不够。
从组合意义的角度考虑这个 DP ,需要关心的只是 \(f_{0,t}\) ,其转移代表选 \(t\) 个数组成序列 \(\{a\}\) ,有 \(f_{0,t} = \sum \binom{n}{a_1} \binom{n-a_1}{a_2} \binom{n-a_1-a_2}{a_3} ...\) ,这其实就是在 \(n\) 个数里面依次选数,选数总数不超过 \(p\) 的方案数。不妨先选出所有要选的数,然后再把这些数分为 \(t\) 个可区分的集合。注意到 \(t\) 个集合之间是两两独立的,那么每个数可以自由放进 \(t\) 个集合中的任意一个集合,集合的划分方案数就是 \(t\) 的总数次方。最终可以得到:
\[R_t = f_{0,t} = \sum_{i=0}^p \binom{n}{i} t^i\]
cf700e
给定串 \(S\) ,找到长度为 \(k\) 的串的序列 \(\{s_i\}\) 满足 \(\forall i \in [2, k]\) ,\(s_i\) 在 \(s_{i-1}\) 中出现至少两次,且 \(s_0\) 是 \(S\) 的子串。求最大的 \(k\) 。
时间复杂度:\(O(|S|\log)\) 。
题解
(未实现)
引理 1
存在一个最优解,满足 \(s_i\) 是 \(s_{i-1}\) 的后缀。
对满足条件的序列前缀长度 \(k\) 应用数学归纳,\(k=1\) 显然成立。对于 \(k\le{2}\) 如果 \(s_k\) 不是 \(s_{k-1}\) 的后缀,不妨把 \(s_{k-1}\) 后面的若干字符删除,直到 \(s_k\) 成为 \(s_{k-1}\) 后缀。注意到任意 \(s_i\) 删除末尾的若干字符后仍然会在 \(s_{i-1}\) 出现至少 2 次。因此可以从 \(k\) 到 \(2\) 不断删除后面末尾若干字符直到满足条件,而 \(s_k\) 不会发生改变,不会影响后面的部分。
引理 2
对于 SAM 上的任一节点 u ,其后缀链接为 v ,v 的任一串在 u 的任一串的出现位置集合都相同。
可以反证。如果有不相同,可以发现对于任意 u 的最长串 \([l, r]\) ,字符 \(l-1\) 是可以唯一确定的,换言之存在更长的串与 u 节点的最长串 right 集合相同,这与 SAM 的性质矛盾。
正题
有了这两个引理,就可以在 SAM 上 DP ,并且只需要考虑从每个节点的后缀链接的转移,如果其后缀链接节点的任一子串在该节点的任一子串中出现至少两次,转移的时候就加一,否则不变。
问题转换为判断一个节点的后缀链接是否在该节点出现至少两次。没有想到什么巧妙的做法,可以线段树维护 right 集合,然后随便从 right 集合拿一个点查询指定区间是否有后缀链接的 right 集合元素。
cf1285f
给定一个值不超过 \(m\) 的正整数集合 \(S\) ,对于所有 \(x, y \in S\) 求 \(\max(\mathrm{lcm}(x, y))\) 。
时间复杂度:\(O(m^{1.5})\) 。
题解
设集合 \(T\) 满足 \(T = \{d | \exists x \in S, d | x\}\) ,那么答案等于对于所有 \(x, y \in T, x \bot y\) 求 \(\max(\mathrm{lcm}(x, y))\) 。
从大到小考虑 \(T\) 的每个数,对于当前数 \(x\) ,设 \(y\) 是与 \(x\) 互质的最大的“可能有用”的值。可以发现一个性质,由于 \(x\) 此时是未考虑的数的最大值,那么 \(\forall x < k < y\) ,\(k\) 在考虑完 \(x\) 之后都不会对答案产生贡献,可以把这样的 \(k\) 从“可能有用”的范畴删去。
那么可以用一个栈 \(R\) 维护所有“可能有用”的值,在普通的栈的基础上还要支持查询是否存在一个与 \(x\) 互质的数从而确定是否需要弹栈,弹完栈后的栈顶就是对应的 \(y\) 。
众所周知互质的条件很好用莫比乌斯函数表示,于是接下来要做的就是套路了:
\[\sum_{y\in{R}} [x\bot{y}] = \sum_{d|x} \sum_{d|y,y\in{R}} \mu(d)\]
维护 \(f(d) = \sum_{d|y,y\in{R}} \mu(d)\) 即可。
at_agc035_f
有一个 \(n \times m\) 的网格,依次执行两个操作:
- 对每一行选择非负数 \(a_i\) ,把该行左边 \(a_i\) 个格子加一。
- 对每一列选择非负数 \(b_i\) ,把该列上边 \(b_i\) 个格子加一。
形式化的,合法网格的格子 \((i, j)\) 的权值为 \([j \le a_i] + [i \le b_j]\) ,求有多少不同的合法网格。
时间复杂度:\(O(n+m)\) 。
题解
(未实现)
每个 \(a_i, b_i\) 随便选的方案数很好算,但是一种合法网格对应多个选取方案。
例如 \(a_i = j, b_j = i - 1\) 和 \(a_i = j - 1, b_j = i\) 对网格的影响是相同的。
引理 1
称一个满足 \(\forall b_j > 0, a_{b_j} \neq j-1\) 的选取方案选取方案是优秀的,所有优秀的选取方案和所有不同的合法网格一一对应。
Part1
每个优秀方案对应的网格不同。
反证法。设两个不同的优秀的选取方案分别为 \(\{a\}, \{b\}\) 和 \(\{c\}, \{d\}\) ,它们对应的网格相同。设 \(j\) 是最小的满足 \(b_j \neq d_j\) 的数,如果不存在这样的 \(j\) ,那么 \(b, d\) 相同,\(a, c\) 不同,对应的网格显然不会相同,矛盾。不妨假设 \(b_j < d_j = i\) ,考虑格子 \((i, j)\) 的权值,必须是 1 ,那么有 \(c_i < j\) 且 \(a_i \ge j\) 。
由 \(c_{d_j} \neq j-1\) 可以得到 \(c_i < j-1\) ,如果 \(j=1\) 显然不存在合法 \(c_i\) 。如果 \(j\ge{2}\) ,由于 \(j\) 是最小的满足 \(b_j \neq d_j\) 的数,有 \(b_{j-1}=d_{j-1}\) ,考虑格子 \((i,j-1)\) 的权值,可以发现并不相等,矛盾。
Part2
每个合法网格存在优秀的选取方案对应。
合法网格对应若干任意选取方案,对于一个不优秀的选取方案,把所有 \(a_i=j-1, b_j=i\) 替换为 \(a_i=j, b_j=i-1\) 即可得到优秀方案。
正题
通过引理 1 ,问题转换为求优秀的选取方案数,直接做比较困难,考虑容斥/反演。对于一个选区方案,称一个 \(j\) 是不优秀位置,当且仅当 \(a_{b_j}=j-1\) 。设 \(f_r\) 表示恰好有 \(r\) 个不优秀位置的方案数,答案就是 \(f_0\) 。
设 \(g_r\) 表示钦定了 \(r\) 个不优秀位置的计算方案数,于是有:
\[\frac{n^{\underline{r}}m^{\underline{r}}}{r!} (m+1)^{n-r} (n+1)^{n-r} = g_r = \sum_{i\ge{r}} f_i \binom{i}{r}\]
二项式反演即可得到 \(f_0\) 的表达式。
lg6596
求 \(n\) 个点的割边不超过 \(m\) 的简单连通图数目,点是可区分的。
时间复杂度:\(O(n^3)\) 。
题解
设 \(f_i\) 表示恰有 \(i\) 条割边的方案数,可以发现如果钦定 \(i\) 个割边,还要保证剩下的 \(i+1\) 个连通块是边双。设 \(g_i\) 表示钦定 \(i\) 条割边的计数方案数,根据 \(g\) 的定义,钦定 \(i\) 条割边后只需要保证剩下 \(i+1\) 个连通块是连通的。而 \(f, g\) 的关系显然是二项式反演。
钦定割边的过程可以转换为先把点划分为 \(i+1\) 个集合,然后它们各自独立,都形成连通块,再在这些点集里连割边。设这些点集的大小组成大小序列 \(\{a\}\) ,那么有:
\[g_i = \sum_{\{a\}} (\prod_k h_{a_k}) (\prod_k a_k) n^{|a|-2}\]
其中 \(h_x\) 表示 \(x\) 个点的连通图数目,\((\prod_k a_k) n^{|a|-2}\) 是连割边的方案数,这个划分集合的过程显然可以用 \(O(n^3)\) 的 DP 描述。
- 求 \(h\) :
设 \(H_x\) 表示 \(x\) 个点的无向图数目,每条边独立,有 \(H_x = 2^{\binom{x}{2}}\) ,枚举一号点的连通块大小,有 \(H_x = \sum_{i=1}^x \binom{x-1}{i-1} h_i H_{x-i}\) 。于是可以 \(O(n^2)\) 求出 \(h\) 。不难发现可以利用多项式科技做到 \(O(n\log)\) ,不在讨论范围内。
- 连割边的方案数:
把每个连通块抽象成一个点,\((i, j)\) 之间连 \(a_i a_j\) 条边,该图的生成树个数就是连割边的方案数,应用矩阵树定理,归纳一下行列式即可得到答案就是 \(n^{|a|-2} \prod_k a_k\) ,过程繁琐,略去。
at_agc023_d
有 \(n\) 个人,第 \(i\) 的人住在数轴的 \(a_i\) 处。所有人在一辆处于 \(S\) 处的车上,人们会投票决定车的移动方向,第 \(i\) 个人可以投出 \(p_i\) 票,司机会为负方向投出半票,每次人数改变后重新投票。每个人会用最优的投票策略最小化到自己的坐车距离,求车的总行驶距离。
时间复杂度:\(O(n)\) 。
题解
不妨假设 \(p_1 \le S \le p_n\) ,\(\{a\}\) 严格单调递增。
引理 1
若 \(p_1 \ge p_n \land S \ge a_{n-1}\) ,车会一直向负方向开直到到达 \(a_1\) 。
对 \(n\)
应用数学归纳法。显然成立,好像负方向的人没有任何理由投正方向的票,而且一定能投赢。
引理 2
若 \(p_1 \ge p_n\) ,车在到达 \(a_n\) 前先到达 \(a_1\) 。
当车在行驶过程中若一直没有到达 \(a_1\) 且正方向只剩下 \(a_n\) 没有到达的时候,根据引理 1 ,此时车会一直往负方向开,先到达 \(a_1\) 。
正题
那么如果 \(p_1\ge{p_n}\) ,第 \(n\) 个人的坐车距离总是第 \(1\)
个人的坐车距离加上一个定值,那么他可以把选票都给第 \(1\)
个人。打不过就抱大腿。反之同理第 \(1\) 个人会把选票给第 \(n\) 个人。于是就可以住转换到 \(n-1\) 的子问题,递归求解直到 \(n=2 \lor S < p_1 \lor S > p_n\)
即可。
at_agc023_f
给定一颗 \(n\) 个点的有根树,每个点有取值在 \(\{0,1\}\) 的点权,求树上拓扑序对应点权序列的最小逆序对数。
时间复杂度:\(O(n\log{n})\) 。
题解
(未实现)
树上拓扑序的问题除了子树合并外,还有另一种考虑方式。
每个点有一个拓扑序列,初始时是其本身。每次选一个非根点,把该点合并到其父亲节点并把其拓扑序列接在父亲节点的拓扑序列后,直到只剩根节点。容易发现此时根节点的拓扑序列和树上拓扑序列一一对应。
这样做的好处是避免了两个子树合并时拓扑序列的相互插入的处理。
定义一个点的重量是其拓扑序列中 0 的数量与 1 的数量的比值。事实上按照重量选点合并就是最优答案。不会证明,证明不会。
cf685c
给定三维空间 \(n\) 个整点 \(P_i\) ,找一个整点 \(Q\) 使得 \(P_iQ\) 的曼哈顿距离的最大值最小,求这个曼哈顿距离。
时间复杂度:\(O(n\log)\) 。
题解
二分答案 \(K\) ,判断是否存在点 \(Q\) 到所有点的曼哈顿距离不超过 \(K\) 。
如果空间是二维,曼哈顿距离转切比雪夫距离后每个维度就独立了。
三维的话 \(Q\) 的覆盖范围是一个正八面体,而切比雪夫距离的覆盖范围在三维是正方体。
加一个维度,把点 \((x, y, z)\) 转换为四维点 \((a, b, c, d) = (x+y+z, x+y-z, x-y+z, -x+y+z)\) ,容易发现两个三维点的曼哈顿距离等于对应四维点的切比雪夫距离。
然后就可以解出 \(Q\) 对应的四维点在每个维度的取值范围,进而判断是否存在三维整点 \(Q\) 。
lg4258
有 \(n\) 个球和 \(m\) 个盒子,每个盒子至多装三个球,每个球必须装进一个盒子里,且每个球有一个集合 \(S_i\) ,第 \(i\) 个球只能放进 \(S_i\) 中的盒子里。
称一个放了不超过一个球的盒子是半空的,求一组方案使得半空的盒子最多。
时间复杂度:\(O((n+m)(m+\sum_{i=1}^n|S_i|)\) 。
题解
(未实现)
容易想到把球和盒子连边转换为图论问题。考虑转换为匹配,每个球必须是匹配点,其匹配的边代表其选的盒子。
盒子就很诡异了,首先一个盒子至多放三个球,那么一个盒子事实上要拆成三个点,其次“半空”的盒子要对答案产生贡献,不妨考虑能否使得半空的盒子增加一条匹配。当然是可以的,一个盒子“半空”意味着三个点中有至少两个非匹配点,那么把这三个点任意连一条边即可。
那么该图的最大匹配数减去 \(n\) 就是答案。特别的是,要保证每个球是匹配点,那么从球开始找增广路即可,如果某个球不存在增广路,说明问题无解。
该图点数 \(n+3m\) ,边数 \(m+\sum_{i=1}^n|S_i|\) 。
th1688-c
有 \(n\) 个球和 \(m\) 个盒子,每个盒子有一个集合 \(S_i\) ,第 \(i\) 个盒子只能放 \(S_i\) 中的球。
定义一个盒子的权值为 \(\lfloor\frac{x}{2}\rfloor\) ,其中 \(x\) 是该盒子内放的球数,求一组方案使得盒子的权值和最大。
时间复杂度:\(O((n+m+\sum_{i=1}^m|S_i|)(m+\sum_{i=1}^m|S_i|))\) 。
题解
\(\lfloor\frac{x}{2}\rfloor\) 实际上就是将该盒子内的点两个分为一组能组成的组数。那么不难想到把一个盒子的 \(S_i\) 中的球两两连边建图,图的最大匹配数就是答案。
但是这样边数会到平方级别,不能接受。需要优化建图。
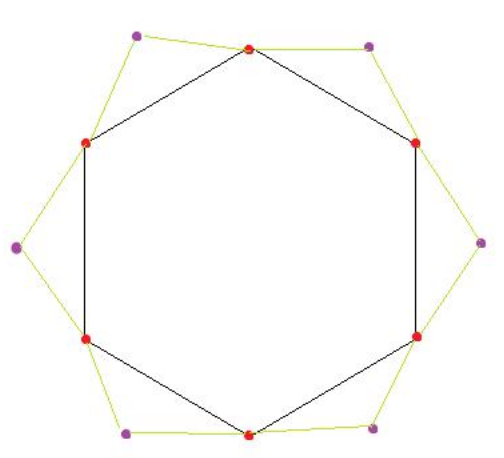
如上图,对应一个 \(|S_i|=6\) 的盒子的连边。紫色点表示球,红色点表示辅助节点,容易发现任意两个紫色点都可以通过辅助点间接匹配,其效果等价于两两连边。
注意要保证红色点数量为偶数,\(|S_i|\) 为奇数的盒子就额外加一个红色点即可。
该图点数不超过 \(n+m+\sum_{i=1}^m|S_i|\) ,边数不超过 \(m+\sum_{i=1}^m|S_i|\) 。
cf1326f2
给定一个长 \(n\) 宽 \(n\) 的 01 矩阵 \(M\) 。
对于一个 \(1\) 到 \(n\) 的排列 \(\{p_i\}\) 和一个长为 \(n-1\) 的 01 序列 \(\{a_i\}\) ,称 \(p\) 在 \(a\) 上合法,当且仅当 \(\forall i \in [1, n - 1], M_{p_i, p_{i+1}} = a_i\) 。
对于所有可能的 \(a\) 求出有多少 \(p\) 在 \(a\) 上合法。
时间复杂度:\(O(p(n) 2^n n + 2^n n^2)\) ,其中 \(p(n)\) 是 \(n\) 的划分数。
题解
既有 1 的限制又有 0 的限制难以直接处理。
这类题有一个套路:忽略一类限制。这里我们忽略 0 的限制。
记 \(A(S)\) 表示 \(a\) 压缩为 \(S\) 时的答案。考虑计算 \(A\) 的父集和 \(B\) ,即 \(B(T) = \sum_{T \subseteq S} A(S)\) ,然后通过反演还原 \(A\) 。那么这样就只有 1 的限制,\(B(S)\) 的意义就是钦定排列一些相邻位置 \(p_i, p_{i+1}\) 满足 \(M_{p_i,p_{i+1}} = 1\) ,而未被钦定的位置没有任何限制。
可以发现,如果将 \(M_{i,j} = 1\) 看作连边 \((i, j)\) ,\(B(S)\) 相当于将排列划分为若干连续段,要求每个段内必须连成一条链。那么对于 \(B(S), B(T)\) ,如果 \(S, T\) 代表的划分本质相同,就一定有 \(B(S) = B(T)\) 。也就是说只需要对于所有 \(n\) 的划分计算 \(B(S)\) 即可。
预处理出 \(f(S)\) 表示用集合 \(S\) 内的点能组成多少条链。那么对于一个划分的答案,就是所有对应长度的点集划分的 \(f\) 的乘积和。枚举点集划分是不可取的,事实上,将对应的 \(f\) 做一个并卷积,最终序列的全集位置的值就是答案。因为确定了长度划分,如果若干集合存在一对有交,它们的并的长度就会小于 \(n\) ,不可能是全集。
具体的,设 \(F_k(S) = [|S| = k] f(S)\) ,那么一个划分的答案就是对应的 \(F_k\) 的并卷积的末项。
loj575
给定一个字符串 \(s_1, s_2, \dots,
s_n\) ,仅包含 < 和 >
两种字符。求「使得 \(p_i < p_{i+1}\)
当且仅当 \(s_i\) 为
< 的排列 \(p_1, p_2, \ldots,
p_{n+1}\)」的数量。
时间复杂度:\(O(n\log^2)\) 。
题解
(未实现)
既有小于号的限制又有大于号的限制难以直接处理。
这类题有一个套路:忽略一类限制。这里我们忽略
> 的限制。
把 > 看做隔板,忽略 >
的限制后唯一的限制是隔板之间的一段数必须单调递增,也就是把 \(n\) 个数填入每一段,设有 \(m\) 段,长度组成序列 \(\{a\}\) ,那么方案数就是
\[\frac{n!}{\prod_{i=1}^m a_i}\]
考虑怎么反演回去,直接一波子集反演的复杂度太大,无法接受。不同于
cf1326f2 的是,这里只需要对于给定的 \(s\)
计算答案。可以应用另一个不知道叫啥的容斥,设 \(f_i\) 表示考虑前 \(i\)
段,每个隔板的左边严格大于右边的所有方案的分母贡献,转移钦定一段后缀合并,有
\(f_i = \sum_{j=0}^{i-1} f_j (-1)^{i-j} \frac{1}{(i-j)!}\) 。
卷积形式,分治 NTT ,答案就是 \(f_m n!\) 。