FKT算法
大一专业课讲的东西,感觉和 OI 沾点边。
课程资料不方便贴出来,可以参考这个。
前置知识:排列和排列的环分解,矩阵和行列式,图论基本概念。
这篇是介绍一下思想和证明,许多说明性的细节被简要概括了(有空的话再完善细节啥的吧)。
引入
如何求一张图的完美匹配的数量?
以下仅考虑 \(|V|\) (点数)为偶数的图 \(G = (V, E)\) ,记 \(n = |V|\) 和 \(m = |E|\) (边数)。
完美匹配是边集的子集 \(M \subseteq E\),满足边的端点不重不漏地覆盖了点集。
\(K_n\) 表示 \(n\) 个点的完全图。
记 \(A\) 为 \(G\) 的邻接矩阵,即 \(A_{ij} = 1\) 当且仅当 \((i, j) \in E\) (\(i\) 到 \(j\) 有连边),否则 \(A_{ij} = 0\) 。
一个想法是,枚举 \(K_n\) 的所有完美匹配 \(M\) ,然后判断 \(M\) 的边是否都在原来的图 \(G\) 中,即是否满足 \(M \subseteq E\) 。 记 \(K_n\) 的完美匹配的集合为 \(PM(n)\) ,则 \(G\) 的完美匹配数量为 \[ ans = \sum_{M \in PM(n)} [M \subseteq E] = \sum_{M \in PM(n)} \prod_{(i, j) \in M} A_{ij} \]
举例,如下图。

(当然这玩意直接拿来算是没有意义的)
Pfaffians
判断 \(M \subseteq E\) 的依据是计算 \([M \subseteq E] = \prod\limits_{(i,j) \in M} A_{ij}\) ,这个值只能是 0 或 1 。
如果将 \(M\) 内的边依次写出来,就可以得到一个 \(V\) 的排列 \(\sigma\) ,这个排列的符号(负一的逆序对数次方)记为 \(\mathrm{sgn}(\sigma)\) ,考虑一个类似的式子 \[ \mathrm{wt}(M, \sigma) = \mathrm{sgn}(\sigma) \prod_{i=1}^{n/2} A'_{\sigma(2i-1), \sigma(2i)} \]
其中 \(A'\) 和 \(A\) 略有不同,它是将邻接矩阵的部分 \(1\) 的位置改为 \(-1\) 使得 \(A'\) 成为一个反对称矩阵:\(A'_{ij} = - A'_{ji}\) 。
那么显然 \(|\mathrm{wt}(M, \sigma)| = [M \subseteq E]\) ,因为它们在式子上只有符号的差异。
虽然定义上不仅与 \(M\) 有关,还与选取的排列 \(\sigma\) 有关,但是有趣的是,无论按照什么顺序写边,按照什么顺序写端点得到的 \(\sigma\) ,算出来的 \(\mathrm{wt}(M, \sigma)\) 都是一样的,因此这个值仅仅与 \(M\) 有关,可以记为 \(\mathrm{wt}(M)\) 。
证明:如果交换两条边的顺序,相当于在排列里交换了两个点两次,那么 \(\mathrm{sgn}(\sigma)\) 不变,同时后边的连乘符号也自然不受顺序影响。
如果交换一条边内两个端点的顺序,在排列里交换了两个点,排列的符号变化,同时后边的连乘符号有一项变化,由于 \(A'\) 是反对称矩阵符号又会变一次,因此总的值不变。
假设可以找到一个 \(A'\) 使得 \(\mathrm{wt}(M) = [M \subseteq E]\) ,那么要求的值变成了 \[ ans = \sum_{M \in PM(n)} \mathrm{wt}(M) \]
上式称为 \(A'\) 的 Pfaffian ,记为 \(\mathrm{Pf}(A')\) 。
反对称矩阵行列式
考虑反对称矩阵 \(A'\) 的行列式 \[ \det(A') = \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma) \prod_{i=1}^n A'_{i,\sigma(i)} \]
如果 \(\sigma\) 存在 \(i\) 使得 \(\sigma(i) = i\) (环分解有自环),那么 \(A_{i,\sigma(i)} = 0\) ,这一项是没有贡献的。
如果 \(\sigma\) 的环分解存在一个非自环的奇环,那么将这个奇环的方向反过来得到 \(\sigma'\) ,注意到 \(\mathrm{sgn}(\sigma) = \mathrm{sgn}(\sigma')\) 且连乘符号的值相反,将 \(\sigma\) 和 \(\sigma'\) 两两一组,每组在行列式中的贡献为 \(0\) 。
综上,我们只需要考虑偶环构成的排列的贡献,记 \(EC(n)\) 是这些排列,有 \[ \det(A') = \sum_{\sigma \in EC(n)} \mathrm{sgn}(\sigma) \prod_{i=1}^n A'_{i,\sigma(i)} \]
而仅有偶环构成的排列和 \(K_n\) 中完美匹配的二元组 \((M_1, M_2)\) 是一一对应的!
将 \(M_1\) 和 \(M_2\) 直接并起来就可以得到一个偶环组成的排列 \(\sigma\) ,其中每个偶环都是由 \(M_1\) 和 \(M_2\) 的边交替构成。偶环上边的方向怎么确定?每个环选定环上编号最小的点,指向 \(M_1\) 中的连边。
注意:\(M_1\) 和 \(M_2\) 的公共边在 \(\sigma\) 中体现为两个点之间的重边组成的二元环。
类似地每个偶环组成的排列 \(\sigma\) 也可以拆分成两个完美匹配 \(M_1, M_2\) 。
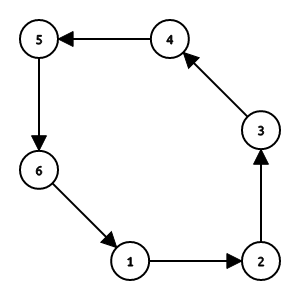
如上图,找到偶环编号最小的点 \(1\) ,然后其指向 \(2\) ,那么 \((1, 2) \in M\) 。然后沿着这个方向把边交替加入 \(M_1, M_2\) 。最终可以知道,这个排列对应的两个匹配为 \[ M_1 = \{(1, 2), (3, 4), (5, 6)\}, M_2 = \{(2, 3), (4, 5), (6, 1)\} \]
这个一一对应关系告诉我们 \(|EC(n)| = |PM(n)|^2\) ,并且枚举 \(\sigma \in EC(n)\) 等价于枚举 \(M_1, M_2 \in PM(n)\) ,于是 \[ \begin{aligned} \det(A') &= \sum_{M_1 \in PM(n)} \sum_{M_2 \in PM(n)} \mathrm{sgn}(\sigma) \prod_{i=1}^n A'_{i,\sigma(i)} \\ &= \sum_{M_1 \in PM(n)} \sum_{M_2 \in PM(n)} \mathrm{sgn}(M_1) \mathrm{sgn}(M_2) \prod_{i=1}^n A'_{i,\sigma(i)} \\ &= \sum_{M_1 \in PM(n)} \sum_{M_2 \in PM(n)} \mathrm{wt}(M_1) \mathrm{wt}(M_2) \\ &= \mathrm{Pf}(A')^2 \end{aligned} \]
(这个等式可以拿上面的例子写一写就很容易明白)
Pfaffian orientation: 找到反对称矩阵
现在我们知道 \(ans = \mathrm{Pf}(A') = \sqrt{\det(A')}\) ,而求行列式是容易的。
但不要忘了第一个等号建立在一个假设上:\(\mathrm{wt}(M) = [M \subseteq E]\) 。现在我们要关注如何找到满足这个条件的 \(A'\) 。
找一个 \(A'\) 等于是给 \(G\) 的边定向,然后把邻接矩阵中正向的定为 \(1\) ,反向的定为 \(-1\) 。我们的目标是让所有 \(G\) 中的完美匹配 \(M\) 满足 \(\mathrm{wt}(W) = 1\) (或全部是负一,这个时候 \(ans = -\mathrm{Pf}(A') = \sqrt{\det(A')}\) ,不影响)。
那么就是让所有 \(G\) 的完美匹配 \(M_1, M_2\) 满足 \(\mathrm{wt}(M_1) \mathrm{wt}(M_2) = 1\) 。上一节的推导告诉我们 \[ \mathrm{wt}(M_1) \mathrm{wt}(M_2) = \mathrm{sgn}(\sigma) \prod_{i=1}^n A'_{i, \sigma(i)} \] 其中 \(\sigma\) 是 \(M_1, M_2\) 对应到的那个偶环构成的排列。
于是我们的要求变为:对于 \(G\) 内任意偶环 \(C\) ,设这个偶环单独构成的排列为 \(\sigma\) , 如果 \(G - C\) 存在完美匹配,那么就要有 \[ \prod_{i=1}^n A'_{i, \sigma(i)} = -1 \]
(注意到每个偶环的符号恰为 \(\mathrm{sgn}(\sigma) = -1\) )。
这个要求是我们目的(\(\mathrm{wt}(M_1) \mathrm{wt}(M_2) = 1\))的充要条件。如果满足了这个要求,那么对于任意偶环构成的排列,将其分解成若干偶环的乘积,从这个要求中可以知道每个偶环的贡献,进而知道偶环构成的排列的贡献恰为 \(1\) 。
如果满足了我们的目的,那么对于任意偶环 \(C\) ,如果 \(G - C\) 存在完美匹配,说明有一个偶环构成的排列包含了 \(C\) ,让 \(C\) 以外的部分全是二元环就可以从 \(\mathrm{wt}(M_1) \mathrm{wt}(M_2) = 1\) 中推出上式(因为每个二元环的贡献都显然是 \(1\) )。
而上式等价于 \(C\) 里面有奇数个顺时针的边和奇数个逆时针的边。
对于一般图这是 #P-Hard 的问题,我们考虑特殊的情况:平面图。
平面图上只需要满足每个面都有奇数条顺时针的边即可。
可以归纳出任何简单环 \(C\) 都满足:顺时针的边数 \(f\) 加上环内部的点(平面上被环围起来的点)数 \(k\) 恰为奇数。
如果 \(C\) 是一个面那么 \(k = 0\) ,这就是我们需要满足的要求。
否则在 \(C\) 内找一条路径把 \(C\) 切成两个环 \(C_1, C_2\) 。\(C\) 是 \(C_1, C_2\) 的对称差,根据归纳假设可以知道 \(f + k\) 为奇数。
现在考虑偶环 \(C\) 。如果 \(G - C\) 有完美匹配那么 \(C\) 的内部必须有偶数个点,于是顺时针的边数必须奇数,证毕。
现在这个问题是相对容易的,任意找一个生成树任意定向,然后就可以逐个确定非树边的方向。
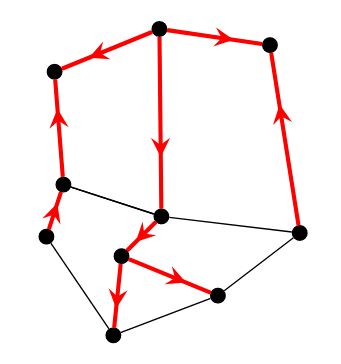
上图找到了一颗生成树 \(T_1\) 并给了一个任意的定向。
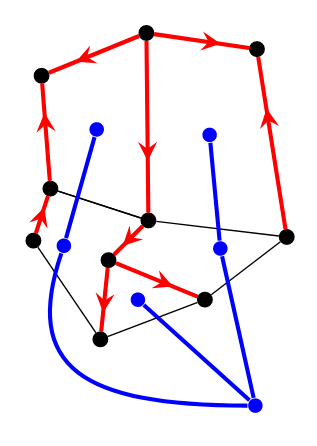
上图找了对偶图的一棵与 \(T_1\) 不相交的生成树 \(T_2\) (这一步在手算定向时可以省略,因为可以肉眼看出哪些非树边可以被定向)。
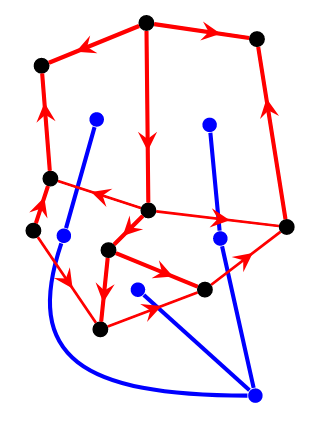
上图从 \(T_2\) 的叶子开始逐步确定 \(G - T_1\) 的定向,使得每个面上都恰有奇数条顺时针边。