KeBlog

总结一些 code-trick ，这种东西看看别人的代码，有时能够大开眼界。

咕咕咕我又来写总结啦。

第一次打牛客，一进牛客发现还有 30s 就有一场比赛，就报了名。
一开始只是打算玩玩，看看牛客的题来着。

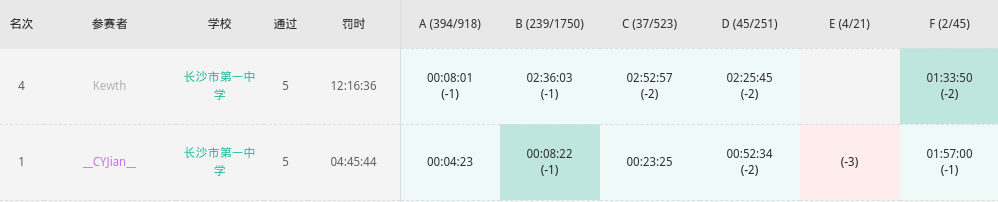
一不小心上瘾了，可惜不计 rating 。
（另外 %%% @CYJian 喜提 rank1 ）

miller-rabin

用于快速测试一个数 \(n\) 是否为质数，有概率出错。

不妨假设 \(n\) 是奇数，此外 miller-rabin 需要随意选取一个小质数 \(p\) 。

理论

miller-rabin 用到的两个基本定理：

• 费马小定理：如果 \(n\) 为质数，一定有 \(p^n \equiv p \pmod{n}\) ，即 \(p^{n-1} \equiv 1\) 。

• 二次探测定理：如果 \(n\) 为质数，对于 \(a^2 \equiv 1 \pmod{n}\) 一定有 \(a \equiv -1\) 或 \(a \equiv n - 1\) 。

以下公式均不给出证明，目的是为了让结论一目了然。

杜教筛一般用于求一类数论函数的前缀和。

假设要求数论函数 \(f(x)\) 的前缀和 \(S(n) = \sum_{i=1}^n f(i)\) 。

杜教筛的关键在于构造两个合适的函数 \(g, h\) 满足 \(h = f \cdot g\) 。

这里的函数相乘指的是狄利克雷卷积。

这里只介绍关于多项式的拉格朗日插值法，对于一般函数的拟合当做一个多项式就好了。

插点值

已知多项式 \(f(x)\) 的 \(n\) 个点值 \((x_i, y_i = f(x_i))\) ，求 \(f(k)\) 。

拉格朗日插值法的思路在于： 对于每个 \((x_i, y_i)\) 找到 \(L_i(x)\) 使得 \(L_i(x_i) = y_i, L_i(x_j) = 0\) ， 其中 \(x_j\) 是已知的 \(x\) 中任意一个不等于 \(x_i\) 的 \(x\) 。

而由 \(L\) 的定义可知，\(f(k) = \sum_{i=1}^n L_i(k)\) 。
代入上式即可求解。

Day -inf (12.06)

thuwc 的报名网站反应是真的慢，中午特意请假去机房填表，结果被这反应速度折服了，一中午还没填完。
好事是，借着这个，我得以手动翘掉了下午的语文课，又跑去机房填表，
网站太慢了，就趁着加载的间隙打了一道题，边听歌边填表边打题，十分舒适。
然后实在是太慢了一节语文课还是不够，算上盖章一不小心把物理课也翘了一半，回来的时候正好全班人围在门口看老师做实验。
目测今年分数线不高，就迷之自信地在 12.06 这个时候就开坑写游记了。

Day1

体验极差，真的就是极差，做梦都没想到 Day1 竟然是这样的。

开考花 30min 交完前面两题，看看时间还剩 3h 。
我觉得换谁在这个处境都会觉得稳得一批，我有三个小时你 Day1T3 能秒我？
我时间都规划好了，花 2h 肝 T3 ，拿 1h 对拍测试检查细节。

• 30min 后：我有一个贪心想法，似乎有理有据
• 1h 后：终于打完了，过了样例，nice 稳了，测测大样例， woc 怎么全 WA 了
• 1.5h 后：（写暴力造数据对拍）妈呀贪心假了，这个只需要怎么怎么随便就卡掉了，这也能过样例
• 2h 后：只剩一个小时了，我要不要写一写链和菊花的暴力啊？算了前面两题应该不会挂，继续肝
• 2.5h 后：（濒临崩溃）我一道联赛题只会 10 分怕不是不要混了，算了还是写暴力吧
• 考试结束 3min 前：（自闭）我 !@#@!%$!@%@@ 暴力怎么这么难打？链的数据怎么死循环啊

考完还听别人说 T1 卡 long long ，我靠，凉凉。
（话说回来考试前一天晚上我还在 OI-Wiki 上偶然翻到了格雷码，看着好复杂心想这玩意学了肯定没用就没看了）

万年卡 E 题系列。

这次 A 竟然不是字符串，开始我已经准备了字符串的输入输出等一堆东西结果发现没卵用
花 1min49 AC ，好像在这之前已经有 12 个人 A 了。

B 第一眼看上去是个 DP ，再看一眼（看成最小值最大）以为是二分，发现是让最大值最大而且还只有三个段后。。。
大力分类讨论！
果然是个分类讨论就巨多细节，判无解判边界判大小 blabla ，结果交 WA 了两发，在 16min AC 。
（ B 最快的 6min 就 A 了，16min 这时候 C 的一血都被拿了的说）

relearn 了一遍 exCRT ，发现之前学的可能是假的（这种情况出现不止一次了 233 ）。

简单来说，中国剩余定理（以下简称 CRT ）主要用于解线性同余方程组：

\[ \begin{equation} \left\{ \begin{aligned} x \equiv a_1 \pmod{m_1} \\\\ x \equiv a_2 \pmod{m_2} \\\\ ... \\\\ x \equiv a_n \pmod{m_n} \\\\ \end{aligned} \right. \end{equation} \]